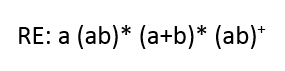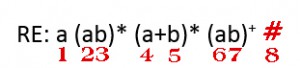SOAL:

Diketahui pusat lingkaran titik A(x₁,y₁) dan titik B (x₂,y₂) serta jari-jari r, maka untuk menentukan titik pada lingkaran  menggunakan persamaan lingkaran.

Sehingga posisi titik terhadap lingkaran terbagi menjadi 3:

k = (x₂-x₁)² + (y₂-y₁)²

• jika k > r² maka titik berada di luar lingkaran
• jika k < r² maka titik berada di dalam lingkaran
• jika k = r² maka titik bersingung pada lingkaran

 

JAWABAN :

Pseudocode :

float x₁, x₂, y₁, y₂,r,k ;

input x₁, x₂, y₁, y₂,r;

k = (x₂-x₁)² + (y₂-y₁)²;

if(k > r²)

print “titik berada di luar lingkaran”;

else if(k < r²)

print “titik berada di dalam lingkaran”;

else

print “titik bersingung pada lingkaran”;

 

Code Generator :

01 mov x2, R0

02 sub x1,R0

03 mul R0,R0

04 mov y2,R1

05 sub y1, R1

06 mul R1, R1

07 add R1, R0

08 mov R0, k

09 mov k, R2

10 mov r,R3

11 mul r,R3

12 gt R3, R2

13 jmpf R2,(16)

14 prt, (titik berada di luar lingkaran)

15 jmp ,(20)

16 mov k, R4

17 lt R3, R4

18 jmpf R4, (21)

19 prt, (titik berada di dalam lingkaran)

20 jmp , (22)

21 prt, (titik bersingung pada lingkaran)

22 …

Website Binus University

Tentukan first, follow, dan production table nya!

1.

SOAL:

S  ->            S + A | S – A | A + S | A – S | B*A

B       ->      aB | B(a+B) | a(a+B) | B*a|b

A      ->       a

S  ->            A+SS’ | A – S S’ | B*AS’

S’     ->       +AS’ | -AS’ | Ɛ

S       ->       AS’‘| B*AS’

S’’      ->     +SS’ | -SS’

B      ->       aBB’ | a(a+B)B’ | bB’

B’      ->      (a+B)B’ | *aB’ |Ɛ

B      ->       aB’’ | bB’

B’’     ->      BB’ | (a+B)B’

A       ->      a

JAWABAN :

S       ->       AS’‘| B*AS’

S’       ->     +AS’ | -AS’ | Ɛ

S’’      ->     +SS’ | -SS’

B        ->     aB’’ | bB’

B’       ->     (a+B)B’ |*aB’| Ɛ

B’’      ->     BB’ | (a+B)B’

A       ->      a

First  S   ={a,b}

First  S’  ={+,-, Ɛ }

First  S’’                ={+,-}

First  B   ={a,b}

First  B’ ={(,*, Ɛ }

First  B’’                ={a,b,(}

First  A  ={a}

Follow S= {$}

Follow S’= {$}

Follow S’’= {$}

Follow B= {*,)}

Follow B’= {*,)}

Follow B’’= {*.)}

Follow A= {+,-,$}

2.

SOAL : 

S-> if E then S |if E then S else S | V:=E

V-> id | id [E]

E-> E+T | E-T | T

T-> T*F | T/F | F

F-> V | (E) | const

JAWABAN : 

S-> if E then S S’ | V:=E

S’-> ε | else S

V -> id V’

V’-> ε |[E]

E-> TE’

E’-> +TE’ | -TE’ | ε

T-> FT’

T’-> *FT’ | /FT’ | ε

F-> V | (E) | const

First (S) = {if, id}

First (S’) = {ε,else}

First (V) = {id}

First (V’) = {ε,[}

First (E) = {id,(,const}

First (E’) = {+,-,ε}

First (T) = {id,(,const}

First (T’) = {*,/,ε}

First (F) = {id,(,const}

Follow (S) = {$,else}

Follow (S’) = {$,else}

Follow (V) = {:}

Follow (V’) = {:}

Follow (E) = {],)}

Follow (E’) = {],)}

Follow (T) = {+,-,]}

Follow (T’) = {+,-,]}

Follow (F) = {*,/,+,-,],}

3.

SOAL:

S -> a = A

A -> aA’ | bA^’

A’ -> +AA’ | Ɛ

JAWABAN :

First S = { a }

First A = { a, b }

First A’ = { +, Ɛ }

Follow S = { $ }

Follow A = { $, + }

Follow A’ = { $, + }

4.

SOAL:

be -> bt be’

be’ -> or bt be’

be’ -> e

bt -> bf bt’

bt’ -> and bf bt’

bt’ -> e

bf -> not bf

bf -> ( be)

bf -> true

bf -> false

Periksalah input sebagai berikut : not (true or false) and true and true and false not (false) true

JAWABAN: 

First (be) = not, (, true, false

First(be’)= or, ε

First(bt)= not, (, true, false

First(bt’)= and, ε

First(bf)= not, (, true, false

 

Follow (be) = {$,)}

Follow(be’)= {$,)}

Follow(bt)= {or,$,)}

Follow(bt’)= {or,$,)}

Follow(bf)= {or,$,), and}

 

 

Website Binus University

Question:
Mengapa di dalam top down parsing tidak boleh ada left recursive dan left factoring?

Answer:

TOP-DOWN PARSING

Dapat dipandang sebagai :

Usaha untuk mencari leftmost deri-vation dari suatu input string
Usaha untuk membangun parse tree dari suatu input string, dimulai dari root (top) sampai dengan leaves (bottom), dengan urutan preorder.
Dalam parser top-down, Left-recursive dan left factor grammars tidak bekerja karena jika terdapat Left-recursion kita tidak tahu kapan recursionnya berhenti ( loop forever ) dan jika terdapat left factor, akan menghasilkan 2 atau lebih produksi ( ambiguitas ). Jadi sebelum melakukan Top-Down parsing, left-recursion harus dihilangkan ( dieliminasi ) dan melakukan left factoring jika terdapat left factor grammar untuk mendapatkan grammar yang sesuai untuk parsing

Contoh :

Pada grammar diatas tidak terdapat left-recursion, tetapi grammar tersebut memiliki left factor sehingga harus dilakukan left-factoring, menghasilkan :

www.binus.ac.id

Task:

Buat RE -> DFA dengan 2 cara:

• Menggunakan cara tree
• Cara ε – NFA

Setelah itu lakukan DFA minimized.

Constraint:

• State dari DFA minimal 5 state dan maksimal 8 state.
• Final state minimal 2 state dan maksimal 3 state

Solution:

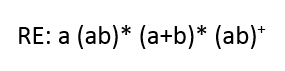
Menggunakan Cara Tree :

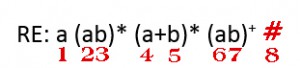
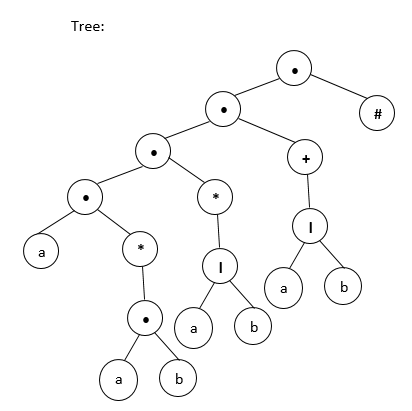
Dari Tree tersebut dapat ditentukan bahwa S₀ atau First postnya adalah 1 , lalu juga diketahui follow postnya sebagai berikut:

Follow post 1 = 2, 4, 5, 6
Follow post 2 = 3
Follow post 3 = 2, 4, 5, 6
Follow post 4 = 4, 5, 6
Follow post 5 = 4, 5, 6
Follow post 6 = 7
Follow post 7 = 6, 8
Follow post 8 = –

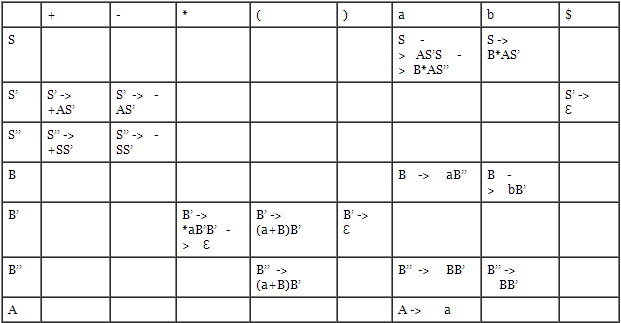
Maka dari itu dapat dibuat tabelnya seperti di bawah ini :

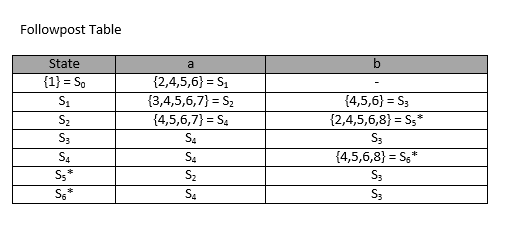
Maka dari bentuk seperti ini didapat DFA seperti ini:

Menggunakan Cara ε – NFA:

Menggunakan cara ini untuk mendapatkan DFA pertama-tama kita buat dulu ε-nfa nya.

Selanjutnya dibuatlah ε-closure nya :

ε-closure (0) = 0 → {S₀}
ε-closure (move(S₀, a)) = ε-closure {1} = {1, 2, 5, 6, 7, 9, 12} → {S₁}
ε-closure (move(S₀, b)) = {}
ε-closure (move(S₁, a)) = ε-closure {3, 8, 13} = {3, 6, 7, 8, 9, 11, 12, 13} → {S₂}
ε-closure (move(S₁, b)) = ε-closure {10} = {6, 7, 9, 10, 11, 12} → {S₃}
ε-closure (move(S₂, a)) = ε-closure {8, 13} = {6, 7, 8, 9, 11, 12, 13} → {S₄}
ε-closure (move(S₂, b)) = ε-closure {4, 10, 14} = {2, 4, 5, 6, 7, 9, 10, 11, 12, 14} → {S₅*}
ε-closure (move(S₃, a)) = ε-closure {8, 13} = {S₄}
ε-closure (move(S₃, b)) = ε-closure {10} ={S₃}
ε-closure (move(S₄, a)) = ε-closure {8, 13} = {S₄}
ε-closure (move(S₄, b)) = ε-closure {10, 14} = {6, 7, 9, 10, 11, 12, 14} → {S₆*}
ε-closure (move(S₅, a)) = ε-closure {3, 8, 13} = {S₂}
ε-closure (move(S₅, b)) = ε-closure {10} = {S₃}
ε-closure (move(S₆, a)) = ε-closure {8, 13} = {S₄}
ε-closure (move(S₆, b)) = ε-closure {10} = {S₃}

Maka dapat dibuat tabel seperti berikut:

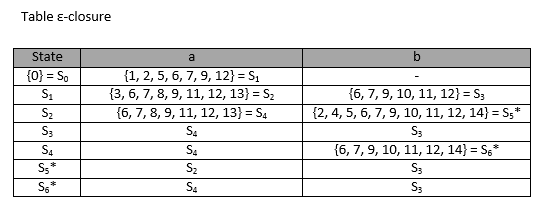
Dari tabel dapat dibuat graph DFA sebagai berikut:

Ternyata dengan menggunakan kedua cara tersebut didapatkan bentuk DFA yang sama, selanjutnya kita akan melakukan minimalisasi DFA menjadi bentuk yang lebih sederhana.

Pertama-tama kita membuat tabel dari DFA yang telah terbentuk, setelah itu pengelompokan state di dalam DFA yang dapat digabung seperti berikut :

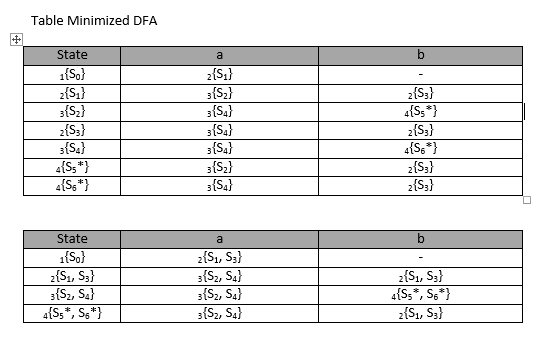
Lalu dibuatlah Graph DFA yang telah diminimalisasi (Minimized DFA)

BINA NUSANTARA UNIVERSITY WEBSITE